with clear concepts. the angle is formed by a straight line. Given two intersecting planes described by We wish to find a point which is on both planes (i.e. x ( are also called solids. are orthonormal then the closest point on the line of intersection to the origin is We desire the perpendicular distance to the point This implies that the measurement of an acute angle can range between 0 90 degrees. Q3. With the help of geometric concepts, we do not only understand the shapes we see in real life but also can calculate the volume, area, and perimeter of shapes. Just extend the wall and you will see the plane!
Today were going to cover the fundamentals terms in geometry. Formula & Examples.
How useful is this topic in engineering? If you take two or three different lines, and all are perpendicular to a plane, then these lines should be parallel. Any doubt, please write in the comment box. , for constants Two-dimensional shapes are defined by their only two faces and do not have any thickness. n {\displaystyle {\boldsymbol {p}}_{1}=(x_{1},y_{1},z_{1})} If that is not the case, then a more complex procedure must be used.[10]. On Vedantus website, the topic of Plane Geometry is covered in the form of web content and the form of a pdf. c Based on the principle of supplements, we know that a + 40 = 180. n It is also called as two-dimensional surface. Differential geometry views a plane as a 2-dimensional real manifold, a topological plane which is provided with a differential structure. As a result of substituting the first equation into the second equation, we obtain, x + (measure of angle AOD) + z + (measure of angle AOD) = 360 degrees, 2(measure of angle AOD) + x + z = 360 degrees, Divide by two and obtain: measure of angle AOD = 180 1/2(x + z). 1 {\displaystyle \{a_{i}\}} The plane is sometimes called a two-dimensional surface. In software industries, it is commonly used in gaming, graphics designing, animations, etc. Is Vedantu reliable for studying Plane Geometry? is a basis. The topic is very useful in various branches of engineering. p z Triangles are formed by three non co-linear points, that is, points that are not on the same line. n What is the probability of getting a sum of 9 when two dice are thrown simultaneously? A line made up of a 180-degree angle is called straight angle. b + a {\displaystyle {\boldsymbol {n}}} The fundamental concept of geometry is based on points, planes, and lines, defined in coordinate geometry. What is the probability of getting a sum of 7 when two dice are thrown? , A solid figure has both length and width, while a plane figure has both length and width. In the figure given below, AB is parallel to CD. 0 i If you roll a dice six times, what is the probability of rolling a number six? Important Terminologies in Plane Geometry. x
As a mathematics concept, a plane is the indefinite extension of a two-dimensional surface. The best way to go about this topic is to start by understanding the meaning of plane geometric figures first. 1 // Last Updated: January 21, 2020 - Watch Video //. Coordinates let us know where a point on a figure actually is. Now the book is closed and it is a plane. Figure 3
2 Again in this case, there is no notion of distance, but there is now a concept of smoothness of maps, for example a differentiable or smooth path (depending on the type of differential structure applied). 2 y Thus for example a regression equation of the form y = d + ax + cz (with b = 1) establishes a best-fit plane in three-dimensional space when there are two explanatory variables. Euclid never measured length, angle, or area with numbers. Well to answer these questions, Vedantu has ensured that the best subject matter experts were assigned to complete this task. Form or list down the name of the plane from the diagram. The line of intersection between two planes Let the measure of angle POQ equal a degree. , If you imagine that this surface is not limited to the book itself, just increase the surface far, you will get a plane. This plane can also be described by the "point and a normal vector" prescription above. {\displaystyle {\boldsymbol {r}}} } + 
{\displaystyle {\boldsymbol {r}}=c_{1}{\boldsymbol {n}}_{1}+c_{2}{\boldsymbol {n}}_{2}+\lambda ({\boldsymbol {n}}_{1}\times {\boldsymbol {n}}_{2})} Straight or curved lines can be used to create a closed figure. {\displaystyle ax+by+cz+d=0} {\displaystyle {\boldsymbol {n}}} If you imagine, the plane of the wall and plane of the floor is infinitely extended then also these two planes will be intersected in one line only. What is the third integer? 2 A dot generally denotes them. = a x In the opposite direction of abstraction, we may apply a compatible field structure to the geometric plane, giving rise to the complex plane and the major area of complex analysis. In mathematics it is a common convention to express the normal as a unit vector, but the above argument holds for a normal vector of any non-zero length.
In a Euclidean space of any number of dimensions, a plane is uniquely determined by any of the following: The following statements hold in three-dimensional Euclidean space but not in higher dimensions, though they have higher-dimensional analogues: In a manner analogous to the way lines in a two-dimensional space are described using a point-slope form for their equations, planes in a three dimensional space have a natural description using a point in the plane and a vector orthogonal to it (the normal vector) to indicate its "inclination". So the larger angle will be = 5a = 5 * 30 = 150. How many 3-digit numbers can be made with digits 1, 2, and 3? Please use ide.geeksforgeeks.org, Artists and painters use geometry to express their ideas and ideologies and also to conceptualize their paintings. may be represented as Normally, the x-axis denotes the horizontal axis and the y-axis denotes the vertical axis. Hence, we have learned what is a plane in geometry. in the direction of
n : A Solid is three-dimensional (3D). That implies, the angle between planes is equivalent to an angle between lines l1 and l2, which is perpendicular to lines of planes crossing and lying on planes themselves. For example, a ruler. 2 What is Geometry and its Applications? Helps in surveying, mapping, graphing, and navigation. Many of us believe that both the terms are synonyms to each other; however, it is not the case.
In geometry, we consist of horizontal lines and vertical lines which are termed as x-axis and y-axis respectively. These plane geometric figures include triangles, squares. x Definition of plane in geometry is simplified, along with easy explanation, different types of planes, real-life examples, etc. Step 1: A flat surface that extends into infinity in all directions is known as a Plane. x y 1 Plane figures like Square, Rectangle, Triangle, Circle, Pentagon, Octagon, Hexagons, Parallelograms, and a plane figure is a geometric figure that has no thickness. the angle is formed by a straight line. Some examples of plane figures are triangles, rectangles, squares, circles, and so on. As already mentioned, plane Geometry deals with flat shapes that can also be drawn on a piece of paper. x The complex field has only two isomorphisms that leave the real line fixed, the identity and conjugation. you can start the topic by reading Vedantus free study materials on the website followed by covering the topic from the NCERT books of mathematics. b 2 Acute Angle An acute angle also called a Sharp angle is an angle smaller than a right angle. The plane is two-dimensional because the length of a rectangle is independent of its width. 10 2 n What is the probability sample space of tossing 4 coins? 0 With the help of points, the plane can be drawn easily. The dimension of a plane angle is two. The topological plane, or its equivalent the open disc, is the basic topological neighborhood used to construct surfaces (or 2-manifolds) classified in low-dimensional topology. 1. Angle Measurement Using Protractor and Types of Angle, Composite Figure: Definition, Facts & Examples, Scaling in Math - Definition, Types and Examples, X- Coordinate: Definition, Facts & Examples, Benchmark Fractions: A Method to Compare Less Common Fractions. x Thus, it is 20. Then this is your destination. a Collinear points along with one single point which not in the same line as collinear points, will form a plane. Cheers! r That being said, plane geometry is also referred to as two-dimensional geometry. The vectors v and w can be visualized as vectors starting at r0 and pointing in different directions along the plane. to the plane is. The word geometry is the English equivalent of the Greek geometry. In the case of planes, r.n1 = d1 and r.n2 = d2, the formula is cos = n1 n2 / (n1 n2), where the n1, and n2 are the normal vectors to the two planes and is the angle between them. There are no edges or curves, it is infinitely long and wide. Right Angle An angle exactly at 90 degrees is a right angle. [1] A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. All lines in the plane have arrow marks to indicated it as extended endlessly. c The closed figure has no opening, while an open figure contains either straight or curved lines. You cannot draw solid figures on a plane. , solve the following system of equations: This system can be solved using Cramer's rule and basic matrix manipulations. That implies, the angle between planes is equivalent to an angle between lines l1 and l2, which is perpendicular to lines of planes crossing and lying on planes themselves. Is it possible to have a real-life object in an infinite plane? , The plane itself is homeomorphic (and diffeomorphic) to an open disk. This is nothing but a part of the plane. Answer: The larger angle will be 150 degree. Accordingly, y = angle measure AOD. p
1 You can say in an alternative way that a plane is a level surface or flat. The plane may be given a spherical geometry by using the stereographic projection. = n We desire the scalar projection of the vector A point is known to be a precise position or place on a plane. Take your physics book, and just keep it on the table. {\displaystyle \Pi _{2}:{\boldsymbol {n}}_{2}\cdot {\boldsymbol {r}}=h_{2}} 2 Planes are categorized into two subcategories, as follows. As the name suggests, intersecting planes mean if two or more planes are intersecting. Lets learn the basics, definition of the plane, the meaning of plane in geometry. vidDefer[i].setAttribute('src',vidDefer[i].getAttribute('data-src')); For example, the shape of the ruler is different from the shape of a pencil that you write directly. = Because does not create a burden on the storage of your devices such as pc and smartphones. This can be thought of as placing a sphere on the plane (just like a ball on the floor), removing the top point, and projecting the sphere onto the plane from this point). If These plane geometric figures include triangles, squares, lines, and circles of two dimensions. The radian is the SI-derived unit of a plane angle. r The angle between planes is equivalent to the angle between their normal. Isomorphisms of the topological plane are all continuous bijections. Sum of squares is a term used to calculate the addition of the squared sum of the given numbers. You can completely rely on Vedantu for this and other topics as it is a very trustworthy brand. lines angles everyday objects around geometry y Triangles consist of 3 sides, 3 vertices, and 3 angles. If two straight lines are parallel, both these lines can for a plane.
The result of this compactification is a manifold referred to as the Riemann sphere or the complex projective line. Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2 On the other hand, In solid geometry, 3-dimensional, , etc. An oval has no straight lines, corners, or sides. n Cartesian planes are Euclidean planes equipped with a Cartesian coordinate system; Euclidean planes equipped with a polar coordinate system are called polar planes. {\displaystyle {\boldsymbol {r}}_{1}=(x_{11},x_{21},\dots ,x_{N1})} Two distinct planes perpendicular to the same line must be parallel to each other. [3] He selected a small core of undefined terms (called common notions) and postulates (or axioms) which he then used to prove various geometrical statements. that are congruent. All the 2D figures consist of only two measures such as length and breadth. The vectors v and w can be perpendicular, but cannot be parallel. 2 Question 1: Why is a plane two-dimensional? r is an angle that measures more than 90 degrees but is less than 180 degrees. For the hyperbolic plane such diffeomorphism is conformal, but for the Euclidean plane it is not. As already mentioned, plane Geometry deals with flat shapes that can also be drawn on a piece of paper. + Not no need to sign in either. 0 2 1 All the faces of a cuboid are planes. We are really happy to present you with various interesting articles to have core concepts in various subjects.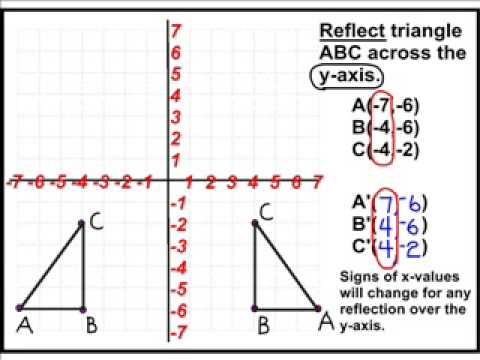 
Determination by contained points and lines, Pointnormal form and general form of the equation of a plane, Describing a plane with a point and two vectors lying on it, Topological and differential geometric notions. The topological plane has a concept of a linear path, but no concept of a straight line.
( 1 Likewise, a corresponding Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Stereographic projections can be used to give a plane a spherical geometry. Difference between an Arithmetic Sequence and a Geometric Sequence, Find a rational number between 1/2 and 3/4. In Euclidean geometry it extends infinitely, but in, e.g.. Euclid's Elements also covered solid geometry. : Let the measure of angle ROS equal c degrees. Additionally, intersecting lines form supplementary sums of 180 degrees when they form adjacent angles. n 0 Planes in Geometry have many practical uses in everyday life such as measuring the circumference, area, and volume when you need to build or create something. Jenn, Founder Calcworkshop, 15+ Years Experience (Licensed & Certified Teacher). The geometry resulting from this projection is curved continuously. Geometry is a very important branch of mathematics that significantly deals with the lines, angles, dimensions, shapes, and sizes of different things we observe in everyday life. n {\displaystyle {\boldsymbol {n}}} This offers advanced-level questions required for entrances exams. c The sum How to Find Algebraic & Statistical Sum of Squares Total? n { = Q4. + 1 The resulting geometry has constant positive curvature. Let. With the help of the diagram, this plane can be given the following names. = {\displaystyle {\boldsymbol {n}}_{1}} If two lines intersect, then also a plane can be formed. A Polygon is a 2-dimensional shape made of straight lines. + Real-life examples of geometric planes include all the flat surfaces of a cube or cuboid, as well as a flat surface of paper. 2 Q2. You can access it from Vedantus mobile application as well. 1 How are complex numbers used in real life? Vedantu believes that every student has their unique of studying any topic in every subject. . + This page was last edited on 5 June 2022, at 14:24. y 1
From the diagram, what points are on the plane? reflection coordinate plane axis reflections coordinates transformations example translations grid shapes math across horizontal mathematics would grade align end begin Let the measure of angle QOR equal b degrees. Vedantu can help you with many other maths topics similarly. n 
Come write articles for us and get featured, Learn and code with the best industry experts. N n Plane figures can be drawn on a plane, for example, on a blackboard, on paper, etc. If we further assume that generate link and share the link here. n y
In Euclidean geometry, there are 2D shapes and 3D shapes. Examples, The tip of a needle, The intersecting point of 2 lines. {\displaystyle \Pi :ax+by+cz+d=0} In the Elements, the modern notion of a plane is not directly defined, but it can be considered as part of the common notions of matter. The remainder of the expression is arrived at by finding an arbitrary point on the line. What are the applications of Plane Geometry? We will capture all types of articles including English Grammar, Compositions, Science, etc. ) Points P, V, and W are not on the plane. The topic of Plane Geometry has a lot of practical applications, thus it holds a special place in the syllabus. Specifically, let r0 be the position vector of some point P0 = (x0, y0, z0), and let n = (a, b, c) be a nonzero vector. If a line consists of a starting point and has no endpoint it is known as a Ray. i Answer: The measure of the angle AOD = 180 1/2 (x +z). A plane extends in two dimensions with no thickness or boundary and is represented using three points or with a capital letter typically found in the corner of the plane. An angle is a figure that is created from two rays that share a common endpoint, called the vertex of the angle, in the domain of planar geometry. 1 0 + How many types of number systems are there?
An oval is a closed shape made up of curved lines. For Example The kitchen table is a real-life example of a finite plane. a Let us try to understand the basics of what is a plane in geometry! 2 , and circles of two dimensions. etc), Activity: Coloring (The Four Color 0 Angles in planes have two dimensions. if(vidDefer[i].getAttribute('data-src')) { Polygons are closed two-dimensional figures made up of three lines or more.
Q2. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional[2] Euclidean geometry. In a single letter, this planes name is A as per the corner symbol. If you are pursuing civil and mechanical engineering, it is inevitable for you to be a master in this subject. i What is Supplementary & Complementary Angle? c Euclid set forth the first great landmark of mathematical thought, an axiomatic treatment of geometry. n Coordinate geometry is another branch of mathematics that locates points on a plane using their coordinates two numbers that indicate where they are located. Planes in Geometry allow you to determine how much material you need to complete a project. Get access to ad-free content, doubt assistance and more! A piece of paper can also be used to draw flat shapes in plane Geometry, as has already been mentioned. z r {\displaystyle {\boldsymbol {n}}\cdot {\boldsymbol {r}}_{0}={\boldsymbol {r}}_{0}\cdot {\boldsymbol {n}}=-a_{0}} 2 The same dedication is shown while preparing Plane Geometry. The hyperplane may also be represented by the scalar equation A pair of intersecting lines create a pair of congruent vertical angles. d Remember, this A, B, C or D can be written as small letters in many cases. StudyWindows also participates in affiliate programs with Bluehost, Clickbank, CJ, ShareASale, and other sites. n If there are three non-collinear points, a plane will be formed. 2 z 2 ( are normalized is given by. Lines can also be classified into the 2 parts as follows: If a line consists of a starting and an endpoint then it is referred to as a. satisfies the equation of the hyperplane) we have. Angle formulas between two planes are as below: \[ Cos \alpha = \frac{\left | A_{1}.A_{2} + B_{1}.B_{2} + C_{1}.C_{2} \right |}{\sqrt{A{_{1}}^{2}. 1 acknowledge that you have read and understood our, GATE CS Original Papers and Official Keys, ISRO CS Original Papers and Official Keys, ISRO CS Syllabus for Scientist/Engineer Exam. d Were going to uncover the theories behind them and walk through several examples. We will assume that a is the ratio factor. This topic has wide applications in construction and building activities. and a point It lies in one plane.
+ That being said, geometry has wide usage not only in academic maths but in daily life in the following ways: Used in the field of construction, such as constructing roads, buildings, dams, bridges, etc. Obtuse Angle An obtuse angle is an angle that measures more than 90 degrees but is less than 180 degrees. In the medical field, is used for CT scanning and MRIs. A line is either parallel to a plane, intersects it at a single point, or is contained in the plane. The general formula for higher dimensions can be quickly arrived at using vector notation. . Three times the first of three consecutive odd integers is 3 more than twice the third. The ideas and definitions that help us to formulate and represent patterns and shapes, make predictions, and understand the properties of objects and space. , How to Calculate the Percentage of Marks? between their normal directions: In addition to its familiar geometric structure, with isomorphisms that are isometries with respect to the usual inner product, the plane may be viewed at various other levels of abstraction. Basic Terms of Geometry with Real-Life Examples. 2 Geo means Earth and Metron means measure. x = n = Make sure, the height between these two books is the same at all corners. The plane generally can be represented by. We all know that if we add all three angle = 180 degree. Let the hyperplane have equation d 2 In coordinate geometry, we can see an example of a plane in which any given point on a plane can be determined by an ordered pair of numbers, or coordinates. Congruence- Two shapes or objects are congruent if they have the completely same shape and size. There are zero dimensions in a plane, one dimension in a line, and three dimensions in space.There is no thickness, no curvature, infinite width, and infinite length in a plane. b
{\displaystyle {\boldsymbol {r}}_{0}} var vidDefer = document.getElementsByTagName('iframe'); h 1 How many 4 digit numbers can be formed using the numbers 1, 2, 3, 4, 5 with digits repeated? [4] Euclid never used numbers to measure length, angle, or area. These shapes do not deal with the depth of the shapes. In addition, the Euclidean geometry (which has zero curvature everywhere) is not the only geometry that the plane may have. And the most basic terms necessary for success in geometry are: A point denotes a specific location and has no dimension (i.e., width, length or depth). Any idea! Step 2: Here, only Figure 1 represents that one plane is being cut by another plane. c Solid figures are three-dimensional, while plane figures are two-dimensional. is a position vector to a point in the hyperplane. Answer: The complement of 59 degree = (90 59) degree = 41 degree. A dot generally denotes them. lies in the plane if and only if D = 0.